The Anatomy of Neural Networks, Part 1
The Journey from Biological Neurons to Artificial Perceptrons
Introduction to Neural Networks: The Biological Inspiration
As we pivot from the high-level overview of supervised learning techniques that have formed the backbone of our recent discussions (link provided below), it’s time to delve into a component of machine learning that stands at the forefront of artificial intelligence: neural networks. In the last several weeks, we have explored various algorithms and their applications, uncovering the layers of complexity and sophistication that enable machines to learn from data. Now, we set our sights on the intricacies of neural networks, a field that not only mimics the workings of the human brain but also harnesses its principles to break new ground in machine intelligence.
The journey into neural networks begins with an appreciation for the biological phenomena that inspire them. Just as the neurons in our brains are interconnected in a complex web of synapses, artificial neural networks are constructed with nodes, often referred to as "neurons," linked together in a web of algorithmic precision. This part of our series will shed light on the transition from biological to artificial systems, explaining how the simple yet powerful structure of a perceptron lays the groundwork for understanding more complex network architectures. We aim to build a robust foundation that will support your growing knowledge as we move from fundamental concepts to the construction of your first neural network model. Stay tuned as we embark on this exciting new chapter, bridging the gap between the abstract wonders of the human mind and the tangible advancements of artificial intelligence.
From Biological to Artificial Neurons
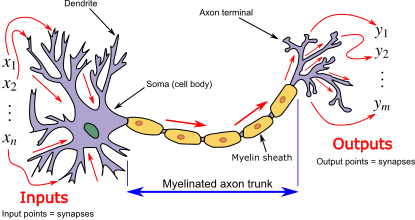
The connection between biological neurons and their artificial counterparts lies at the heart of how neural networks function. In our brains, neurons are the workhorses of thought, sensation, and movement, communicating through electrical and chemical signals. Each biological neuron receives input signals from its dendrites and, if sufficiently stimulated, sends an output signal along its axon to other neurons. This process of synaptic transmission is elegantly mirrored in the design of artificial neural networks.
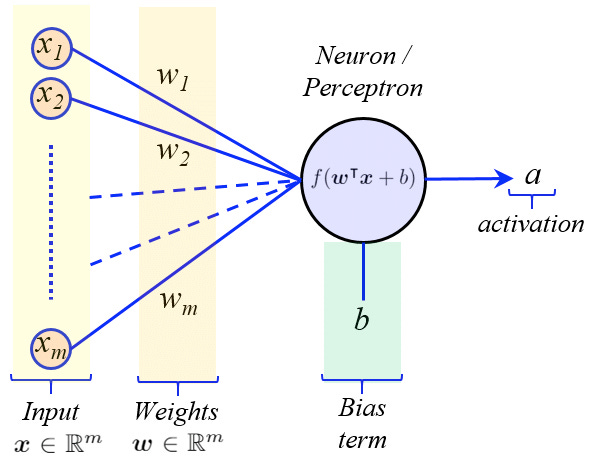
An artificial neuron, or perceptron, emulates this biological concept by receiving multiple inputs, assigning weights to signify the importance of each input, much like the varying strengths of synapses in the human brain. A bias is added to the weighted sum, adjusting the threshold at which the neuron is activated. This is akin to the neuron's response threshold in biological systems, providing a degree of control over its sensitivity. The perceptron then processes these inputs through an activation function, which determines the output. Activation functions introduce non-linearity, allowing the network to solve complex problems that linear equations cannot.
The true power of artificial neurons becomes apparent when they are connected to form a network. Individually, they perform simple tasks, but together, they can approximate any function and solve highly intricate problems. They are organized in layers that process inputs at varying levels of abstraction, from simple patterns to complex features, mirroring the way our brains process information from the general to the specific. This layered approach allows the neural network to learn from vast amounts of data, making decisions, and uncovering patterns far too complex for any single neuron.
Artificial neural networks, inspired by the biological structures in our brains, bridge the gap between biology and computation. By distilling the essence of neural activity into mathematical models, they serve as powerful tools for a myriad of applications in artificial intelligence. From recognizing faces to translating languages, the principles of neural communication continue to guide the advancement of machine learning, enabling algorithms to learn and adapt with a semblance of human-like intelligence.
Basic Neural Network Architecture
When we peel back the layers of complexity in a neural network, we find an architecture that is striking in both its simplicity and its depth. A basic neural network is organized into a series of layers, each composed of individual units called neurons or nodes, and it's here where the magic of learning from data begins to take shape.
Layers of a Neural Network
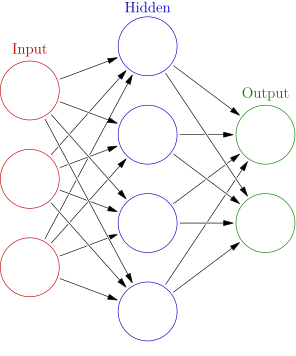
The typical starting point for understanding a neural network's architecture is to look at its layers. There are three primary types of layers in a standard feedforward network: the input layer, hidden layers, and the output layer.
The Input Layer: This is the entry point of the network. Each neuron in this layer represents a feature of the input data. If we're processing images, for instance, each input neuron might correspond to the intensity of a pixel. For tabular data, each neuron would correspond to a column in the dataset.
The Hidden Layers: After the input layer comes one or more hidden layers. These layers are not directly exposed to the input or output and can be thought of as the "processing units" of the network. They contain an arbitrary number of neurons, and each of these neurons is connected to all the neurons in the previous layer. It's within these interconnections that the network forms its complex mappings, with each neuron learning to recognize increasingly abstract features. The depth and width of these layers can vary, significantly impacting the network's learning capacity.
The Output Layer: The final layer is the output layer, which has as many neurons as there are outputs to predict. For classification tasks, this often corresponds to the number of classes. In a regression task, there might be just a single output neuron. The output layer synthesizes the information that has been learned throughout the network and transforms it into a format suitable for the problem at hand.
The Role of Neurons
Each neuron is a fundamental processing unit of the neural network. It receives input from multiple other neurons, processes it, and passes on its output. Inside a neuron, the magic is quite mathematical; the inputs are multiplied by weights – a set of parameters that the network adjusts through learning – and then summed together. This sum is then passed through what is called an activation function.
Activation Functions
Activation functions are vital to a neural network's ability to capture complex patterns. They introduce non-linear properties to the network, which allows for learning non-linear relationships in the data. We will discuss these more in-depth below.
The design and depth of the architecture, the choice of activation function, and the way the neurons are interconnected define the network's ability to learn from complex datasets. By tuning these parameters, a practitioner can coax the network to model an astonishing variety of patterns and relationships within data. However, the true beauty of neural networks lies not just in their structure, but in their adaptability. Through the process of learning, they adjust the weights of each neuron's connections, allowing the network to make better and more nuanced predictions or decisions. This is the core of the network's architecture, a finely balanced dance between structure and flexibility, enabling the neural network to adapt to the data it's given and perform tasks that range from simple pattern recognition to complex decision-making.
Activation Functions in Neural Networks
As we briefly covered above, activation functions play a pivotal role in neural networks by introducing non-linear properties to the system, which enables the network to learn more complex tasks beyond what a linear equation could handle. Essentially, without non-linearity, a neural network with many layers would still function as a single-layer perceptron because summing these layers would give us just another linear function.
The Role of Activation Functions
An activation function decides whether a neuron should be activated or not, determining the output of that particular neuron to the next layer. It works by calculating a weighted sum of the inputs, adding a bias, and then deciding whether and to what extent that signal should progress further through the network.
Types of Activation Functions
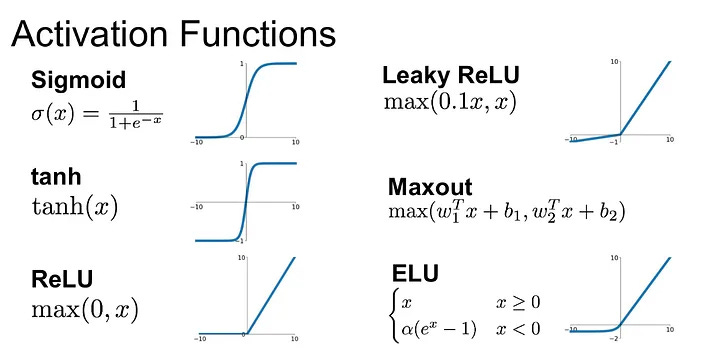
Sigmoid/Tanh Function: The sigmoid function, also known as the logistic function, was historically the most common choice. It maps any input into a value between 0 and 1, which is beneficial for models where we need to predict the probability as an output since the probability of anything exists only between the range of 0 and 1. Its cousin, the hyperbolic tangent function, or tanh, varies from -1 to 1 and is also s-shaped.
While these functions were foundational in the early development of neural networks, they are less commonly used today due to certain drawbacks, such as the vanishing gradient problem, which occurs during backpropagation when layers have very small or large weights and the gradient tends to disappear or "vanish," causing the network to learn very slowly or stop learning altogether. This is something we will cover later in the series.
ReLU Function: The Rectified Linear Unit, or ReLU, has become the default activation function for many types of neural networks because it solves the vanishing gradient problem, allowing models to learn faster and perform better. ReLU is half rectified, meaning that for negative input, it outputs zero, while for any positive value, it outputs that value directly. This simplicity leads to efficient computation and faster training.
However, ReLU is not without its issues; for instance, it can suffer from the "dying ReLU" problem where neurons can become inactive and only output zero if they fall into the negative side of the ReLU function during training.
Leaky ReLU and Variants: To combat the dying ReLU problem, variations such as Leaky ReLU were introduced. These allow for a small, non-zero gradient when the unit is not active, thus allowing for a form of "leak" and helping to alleviate the problem of dead neurons.
Softmax Function: In classification problems, particularly when they are multi-class, the softmax function is typically applied to the final layer of a neural network. It squashes the outputs of each unit to be between 0 and 1, like the sigmoid function. But importantly, it also divides each output such that the total sum of the outputs is equal to 1, making the outputs interpretable as probabilities.
Choosing the Right Activation Function
Selecting the correct activation function for a neural network is crucial and can depend on several factors, including the complexity of the problem, the architecture of the network, and the desired speed of training. While ReLU and its variants are generally a good starting point due to their computational efficiency, it's important to experiment with different functions and to consider the unique aspects of the task at hand.
In practice, it's common to see ReLU used in the hidden layers of a network due to their simplicity and efficiency. For output layers, softmax is popular for multi-class classification tasks, and sigmoid can be used for binary classification.
In conclusion, while activation functions may seem like a simple switch in a network, they're fundamental to the neural network's ability to capture and model complex patterns. The ongoing research in activation functions continues to evolve, driving forward the potential for more complex and capable neural network architectures.
Conclusion
As we reach the conclusion of this first installment on neural networks, we've touched on the fascinating transition from biological inspiration to artificial replication. The analogy of how the human brain's neurons inspired the design of artificial neurons lays a foundation for appreciating the sophistication behind neural networks. With this understanding, we ventured into the structural basics of neural networks, highlighting how individual neurons connect to form a network capable of learning from data.
Looking ahead to our next discussion, we will jump into the dynamic process of forward propagation—the journey of input data through the hidden layers of a network, transformed by weights and activated by functions, culminating in an output that constitutes the network's prediction. We will unravel the complexities of backpropagation, where the network learns from its errors and adjusts its weights to improve accuracy. This intricate dance of adjustments is the heart of a neural network's learning process. And finally, we'll take the leap from theory to practice. You'll get to translate these concepts into code, constructing your very first neural network using PyTorch. This upcoming exploration will not only solidify your understanding but will also empower you to begin crafting your own intelligent systems. Stay tuned as we transition from conceptual to practical, where abstract ideas become tangible lines of code that breathe life into machine intelligence.
References:
Russell, S. J. and Norvig, P., Artificial Intelligence: A Modern Approach, 4th Edition, Prentice Hall, 2021