Collaborative Filtering: The Core of AI Recommendations, Part II
Deepening Our Understanding in AI-Driven Recommender Systems
Introduction
Thank you to everyone who cast their vote in last week's poll about future content directions. The results indicate an eagerness to explore the realm of Generative AI. In a few weeks, we will set off on this exciting journey with an introduction to the foundational concepts of Generative AI, starting with the basics and key distinctions. Our first deep dive will be into Generative Adversarial Networks (GANs), an area that has seen groundbreaking developments. From there, we'll progress to understanding the intricacies of Variational Autoencoders (VAEs) and the mechanics of autoregressive models. This series will also spotlight the transformative impact of Transformer models in generative tasks, highlighting their versatility beyond text generation. Your input has been invaluable in shaping this series, and I'm looking forward to navigating the depths of Generative AI together, uncovering its principles, challenges, and vast potential.
Diving Deeper into Collaborative Filtering
Welcome back to our journey through the fascinating world of recommender systems in AI/ML. Last week, we laid the foundation by exploring what recommender systems are and why they're pivotal in today's digital landscape. We covered various types of recommender systems, from collaborative filtering to content-based and hybrid methods, and touched upon some key challenges like handling sparse datasets, scalability issues, and the delicate balance between personalization and user privacy. If you missed it, I highly recommend last week’s post to get up to speed.
This week, we're diving deeper into the heart of one of the most popular and widely implemented techniques in recommender systems: Collaborative Filtering. You might recall from our previous discussion that collaborative filtering focuses on building recommendations based on the wisdom of the crowd. It's like asking your friends for movie recommendations, but on a much larger, algorithm-driven scale.
We will dissect collaborative filtering to understand its inner workings, starting with its two main flavors: User-Based and Item-Based Collaborative Filtering. Each has its strengths and scenarios where they shine, and we'll explore these in detail. But, as with any powerful tool, there are challenges and limitations. We'll address these head-on, discussing the notorious cold start problem and data sparsity issues, and how they can impact the performance of a recommender system.
By the end of this week's post, you'll have a solid grasp of collaborative filtering's mechanics and be better equipped to appreciate its role in the recommender systems you interact with daily, whether while shopping online, browsing your favorite streaming service, or even exploring new music.
Advanced Perspectives on User-Based and Item-Based Collaborative Filtering
In our previous discussion, we laid the groundwork for understanding user-based and item-based collaborative filtering. Now, let's jump into the advanced aspects that significantly impact their performance and practical applicability.
User-Based CF: Optimizing for Performance
In user-based collaborative filtering, the crux lies in accurately measuring the similarity between users. This involves:
Fine-Tuning Similarity Metrics: The choice of similarity metric can dramatically impact the recommendations. Metrics like cosine similarity, Pearson correlation, and adjusted cosine similarity are commonly used. Adjusting these metrics for specific scenarios, like normalizing for user rating scale variability, can enhance recommendation relevance.
Scalability Solutions: One of the biggest challenges with user-based CF is scalability, as the computational complexity increases with the user base. To tackle this:
Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) can reduce the number of dimensions while preserving the essential characteristics of the dataset.
Clustering: Grouping similar users into clusters can reduce the computation required for similarity calculations. Clustering algorithms like K-means or hierarchical clustering can be used for this purpose.
Item-Based CF: Enhancing Recommendations
Item-based collaborative filtering, on the other hand, focuses on the relationships between items, offering a different set of advantages and challenges:
Computing Item Similarity: The key to item-based CF is determining how items are similar to each other. This can be achieved through:
Advanced Techniques: Beyond the basic correlation measures, more sophisticated methods like association rule mining can uncover deeper relationships between items. Machine learning models, especially those using neural networks, can also be used to learn item similarity from complex datasets.
Dynamic Adaptation: The real world is not static; user preferences change, and new items are constantly introduced. Therefore, item-based CF systems must be dynamic:
Real-Time Updates: Implementing real-time update mechanisms allows the system to quickly incorporate new user interactions, keeping the recommendations fresh and relevant.
Handling Evolving Catalogs: Techniques like content-based filtering can complement item-based CF to handle new items more effectively, using item attributes to bootstrap the recommendation process before enough user interactions are gathered.
By understanding and addressing these advanced aspects of user-based and item-based collaborative filtering, we can significantly enhance the effectiveness and efficiency of our recommender systems. These optimizations and techniques ensure that the systems remain scalable, accurate, and adaptable to the ever-evolving landscape of user preferences and item catalogs.
The Mathematics Behind Collaborative Filtering
In the realm of collaborative filtering (CF), accurately determining the similarity between users or items is crucial. This section delves into three key similarity measures: Cosine, Jaccard, and Pearson correlation, each playing a vital role in the efficacy of recommendation systems.
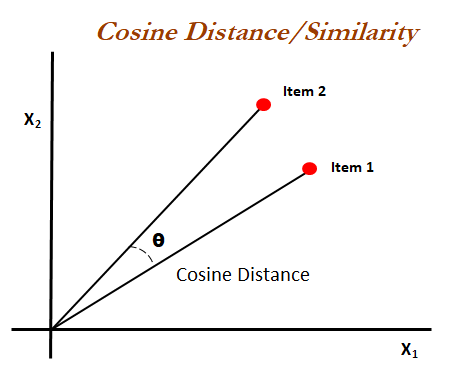
Cosine Similarity
Cosine similarity measures the cosine of the angle between two non-zero vectors in a multi-dimensional space. In CF, these vectors often represent users or items with their ratings as dimensions.
The formula for cosine similarity is:
where A and B are vectors, A⋅B is the dot product, and ∥A∥ and ∥B∥ are the magnitudes of vectors A and B, respectively. Cosine similarity values range from -1 to 1, where 1 indicates perfect similarity.
Jaccard Similarity
Jaccard similarity, or the Jaccard index, is used for gauging the similarity and diversity of sample sets, particularly useful in binary data scenarios (like purchases: bought/not bought).
The Jaccard similarity is calculated as:
Here, A and B are sets, and ∣A∩B∣ and ∣A∪B∣ represent the cardinality of the intersection and union of the sets, respectively.
Pearson Correlation
Pearson correlation measures the linear correlation between two variables and is often used in CF to find the linear relationship between users' ratings.
The Pearson correlation coefficient is computed as:
where Xi and Yi are individual sample points, and X-bar and Y-bar are the means of the samples.
Introduction to Matrix Factorization
Matrix factorization is a cornerstone technique in collaborative filtering, particularly effective for large-scale datasets.
Concept of Matrix Factorization
Matrix factorization involves decomposing the user-item interaction matrix into two lower-dimensional matrices. This decomposition uncovers latent features underlying the interactions between users and items, representing them as vectors in a latent space.
Types of Matrix Factorization
Two popular methods are:
Singular Value Decomposition (SVD): It factorizes the original matrix into three matrices (U, Σ, V). While effective, it's computationally intensive, especially for large matrices.
Alternating Least Squares (ALS): This method iteratively optimizes the factorization by keeping one matrix constant while optimizing the other. It’s particularly suited for large, sparse datasets.
Matrix factorization techniques have been crucial in improving the accuracy and scalability of collaborative filtering systems, addressing challenges like the cold start problem and data sparsity. By reducing dimensionality and uncovering latent factors, they provide a more nuanced and efficient approach to making recommendations.
Mathematical Foundations: Discussion on Challenges
Cold Start Problem
The cold start problem in recommender systems refers to the difficulty of providing accurate recommendations when there is insufficient data about users or items. This challenge is particularly pronounced in two scenarios:
New Users (User Cold Start): When new users join the platform, the system lacks historical data to analyze their preferences. Traditional collaborative filtering approaches struggle here because they rely heavily on past user-item interactions.
New Items (Item Cold Start): Similarly, newly added items lack interaction history, making it challenging for the system to recommend them to the right users.
Addressing the Cold Start Problem
Leveraging User Demographics: For new users, demographic information like age, gender, location, etc., can be used to make initial recommendations based on the preferences of similar demographic groups.
Item Attributes and Content-Based Filtering: For new items, content-based methods that use item attributes (like genre in movies, author in books) can help in making initial recommendations.
Hybrid Approaches: Combining collaborative and content-based filtering can mitigate the cold start problem by utilizing the strengths of both methods.
Data Sparsity Issue
Data sparsity occurs when the user-item interaction matrix has a large number of missing values. This is a common issue in real-world scenarios where each user interacts with only a small subset of items.
Overcoming Data Sparsity
Matrix Factorization Techniques: Techniques like Singular Value Decomposition (SVD) can be used to approximate the missing values in the interaction matrix, helping to alleviate the sparsity issue.
Utilizing Implicit Feedback: Besides explicit ratings, implicit feedback like click history, browsing time, etc., can be utilized to fill in the gaps in sparse data.
Neighborhood Models: Adjusting the size and selection criteria of the user/item neighborhood in collaborative filtering can help address sparsity by focusing on more relevant interactions.
Hybrid Approaches
Hybrid recommender systems combine multiple recommendation techniques to leverage their respective strengths and offset their weaknesses. The goal is to improve recommendation quality and robustness.
Implementing Hybrid Systems
Model-Based and Memory-Based Hybridization: Combining model-based methods (like matrix factorization) with memory-based methods (like nearest neighbors) can balance prediction accuracy and the ability to handle new users/items.
Content and Collaboration Hybridization: Integrating content-based and collaborative filtering approaches helps in dealing with both cold start and sparsity issues.
Utilizing Deep Learning: Deep learning models, especially those employing neural networks, can effectively integrate various types of data (user, item, contextual) for enhanced recommendation quality.
Conclusion
As we conclude our deep dive into collaborative filtering, we've journeyed through the intricate labyrinth of user-based and item-based methods, unraveling the complex mathematics that powers these systems. From exploring various similarity measures like cosine, Jaccard, and Pearson to discussing matrix factorization techniques, we've seen how collaborative filtering forms the backbone of many modern recommender systems.
One key takeaway is the versatility and adaptability of collaborative filtering in different contexts, whether in the realm of e-commerce, streaming services, or social networking platforms. However, as we've also seen, this approach is not without its challenges. The cold start and data sparsity issues are significant hurdles, prompting the exploration of hybrid systems that combine the strengths of different recommendation strategies.
Teaser for Week 3: Building a Recommender System with PyTorch
Next week, we're gearing up for an exciting shift from theory to practice. We'll be stepping into the world of PyTorch, a leading framework in the AI/ML community, known for its flexibility, efficiency, and user-friendly interface.
In the third installment of the series, we'll embark on a hands-on journey to build our very own recommender system using PyTorch. This practical guide will cover everything from setting up your environment to data preprocessing, model creation, training, and evaluation. Whether you're a seasoned PyTorch user or new to the framework, this guide will provide valuable insights into the practical aspects of building and deploying a recommender system.
References
Pablo Castells, Dietmar Jannach. Recommender Systems: A Primer, 2023. https://doi.org/10.48550/arXiv.2302.02579
Yang Li, Kangbo Liu, Ranjan Satapathy, Suhang Wang, Erik Cambria. Recent Developments in Recommender Systems: A Survey, 2023. https://doi.org/10.48550/arXiv.2306.12680.
Sumaia Mohammed AL-Ghuribi, Shahrul Azman Mohd Noah. A Comprehensive Overview of Recommender System and Sentiment Analysis, 2021. https://doi.org/10.48550/arXiv.2109.08794.