Adversarial Search
The Competitive Edge of AI Decision-Making
Introduction
Adversarial search is a fascinating subset of artificial intelligence that plunges into the realm of competitive decision-making. Building on our previous exploration of game theory—a subject that eloquently fuses mathematics, economics, and computer science—we turn our focus to the specialized algorithms and techniques that simulate strategic rivalry and cooperation among intelligent agents.
But why should we care about adversarial search? For one, it's ubiquitous in real-world applications. Whether it's a hedge fund employing high-frequency trading algorithms to outsmart competitors or cybersecurity systems dynamically countering intrusive actions, adversarial search techniques are at the heart of such operations. These methods are also fundamental in simpler contexts, like board games or puzzle-solving, serving as ideal grounds for research and development in AI.
In this post, we will dissect the mechanics of adversarial search, moving from its theoretical underpinnings to its practical implementations. We'll explore a range of algorithms, evaluate their effectiveness, and touch upon the challenges they present. Through this deep dive, we aim to illuminate how adversarial search isn't just about one-upping an opponent—it's about problem-solving, optimization, and making intelligent decisions in complex, dynamic environments.
Join us on this riveting journey into adversarial search, a world where competition meets computer science, and strategic depth fuses with computational rigor. By the end of this post, you'll gain a comprehensive understanding of how adversarial thinking shapes the algorithms that increasingly influence our lives.
The Nature of Adversarial Problems
Characteristics Distinguishing Adversarial Search Problems
In the world of search algorithms, adversarial search problems introduce a layer of complexity that transcends the challenges found in standard optimization or pathfinding problems. Unlike simpler search problems where the objective is clear-cut—such as finding the shortest path or highest utility value—in adversarial scenarios, the objective is dynamic and contingent on the actions of opposing agents. Here, your gain is often your opponent's loss, and vice versa.
Importance of Opponent Modeling
Understanding your opponent's strategy is a cornerstone of adversarial search. In a game like chess, anticipating your opponent's moves can be just as crucial as planning your own. Algorithms designed to solve adversarial problems often incorporate techniques to model or predict an opponent's actions based on their observed behavior or a set of assumed strategies.
Incomplete and Complete Information
Adversarial games can be categorized based on the availability of information:
Complete Information Games: Games like chess or tic-tac-toe, where the entire state of the game is visible to all players.
Incomplete Information Games: Games like poker, where certain elements, such as the opponent's hand, are hidden.
Each category demands its own set of search strategies and considerations, adding layers to the complexity of the algorithmic solutions needed.
Time-Bounded Decisions
In real-world applications and even in board games, decisions often have to be made within a certain time frame. This constraint adds another layer of complexity, requiring algorithms that can produce good-enough solutions within the allotted time.
Stochastic Elements
Some adversarial problems introduce stochastic or random elements into the mix, further complicating the decision-making process. Here, strategies must be robust not just against adversarial actions but also against the uncertainty introduced by these random elements.
Types of Games Suited for Adversarial Search
Adversarial search is particularly well-suited for modeling and solving various types of games that involve elements of competition, strategic interaction, and sometimes even cooperation among players. In this section, we'll explore the types of games where adversarial search algorithms are most commonly applied.
Two-Player Zero-Sum Games
In these games, one player's gain is precisely balanced by the other player's loss. The sum of the utilities for all players is zero, hence the term "zero-sum." Examples include Chess, Tic-Tac-Toe, and Go. Adversarial search algorithms like Minimax and Alpha-Beta pruning are commonly used in these types of games.
Multiplayer Games
While many traditional board games are designed for two players, some games involve three or more participants. Examples include multiplayer card games or political strategy games. In these scenarios, adversarial search becomes more complex, but methods like Monte Carlo Tree Search (MCTS) can still be employed, albeit with adaptations to account for multiple agents.
Partial Information Games
Games like Poker or Battleship are characterized by incomplete knowledge of the game state. Players must make decisions based on imperfect information, introducing an element of uncertainty into the search process. Algorithms like Expectiminimax and Bayesian approaches are particularly useful for these types of games.
Stochastic Games
In some games, elements of chance, such as dice rolls in Backgammon, add a layer of unpredictability. This randomness demands specialized search algorithms, often adaptations of standard techniques, to handle probabilistic outcomes.
Continuous Games
While many games have a finite set of states or moves, some games involve continuous action spaces, as seen in various simulation or real-world applications like robotic motion planning. These types of games often employ advanced techniques, such as neural networks or reinforcement learning, to manage the vast search space.
Cooperative Games
Although the term "adversarial" implies competition, adversarial search algorithms can also be adapted for cooperative multi-agent scenarios. Here, the algorithms aim to find mutually beneficial strategies rather than exploiting opponent weaknesses.
Asymmetric Games
In these games, the set of actions available to each player is different, often significantly so. Asymmetric games pose unique challenges for adversarial search, as algorithms must consider different action and state spaces for each player. Examples include various types of role-playing games or strategic war games.
By understanding the characteristics of these different game types, we can better appreciate the adaptability and range of adversarial search algorithms. Whether dealing with incomplete information, multiple players, or even cooperative objectives, adversarial search continues to provide powerful tools for solving complex problems in game theory and AI.
Basic Algorithms
Adversarial search algorithms form the backbone of decision-making in competitive scenarios. From chess-playing bots to financial prediction algorithms, these algorithms navigate the strategic landscape to find optimal or near-optimal solutions. In this section, we will discuss some foundational algorithms and techniques that are central to adversarial search.
Minimax Algorithm
The Minimax algorithm is one of the earliest and most straightforward techniques for adversarial search. It operates on the principle that one player aims to maximize their score, while the other aims to minimize it. The algorithm recursively explores the game tree, selecting the move that leads to the maximum payoff under the assumption that the opponent will try to minimize it.

Alpha-Beta Pruning
Building on Minimax, Alpha-Beta Pruning is an optimization technique that significantly reduces the number of nodes evaluated in the search tree. By keeping track of the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of (alpha and beta), the algorithm prunes branches that cannot improve the outcome, thereby improving efficiency.
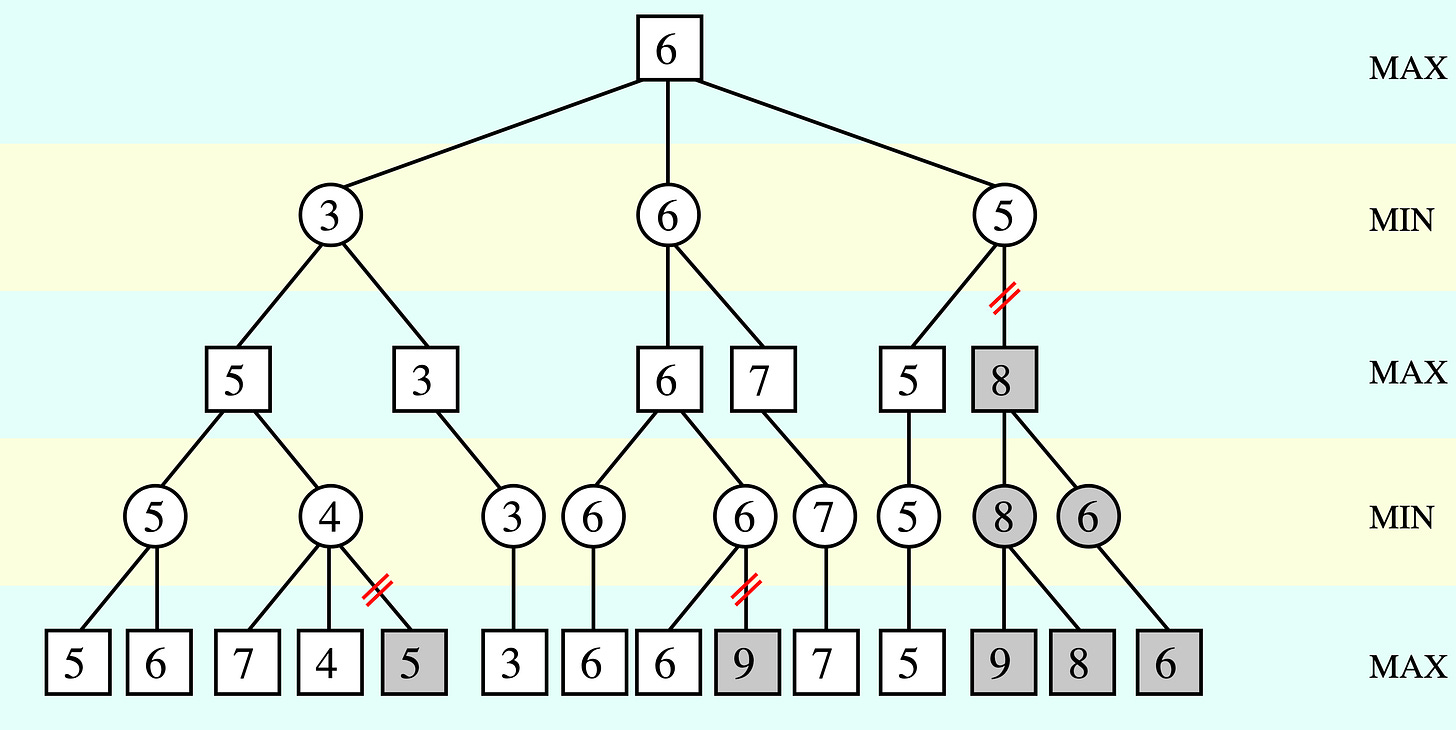
Monte Carlo Tree Search (MCTS)
Unlike Minimax and Alpha-Beta Pruning, MCTS uses statistical sampling to evaluate game positions. By running many simulated games and backing up the results, it gradually builds a search tree that represents the most promising moves. MCTS is particularly effective in games with large or complex search spaces, such as Go.

Successive Elimination of Dominated Strategies (SEDS)
Successive Elimination of Dominated Strategies is a technique used to simplify the strategic landscape of a game. A dominated strategy is one that performs worse than another strategy in all possible scenarios for a player. By eliminating these inferior choices, we can reduce the size of the strategy set that needs to be evaluated, making the search process more efficient.
Definition and Importance: The concept involves iteratively removing dominated strategies from the game's normal form representation. It is particularly important in simplifying complex games with numerous strategies, helping algorithms navigate through smaller, more relevant search spaces.
How it Simplifies Game Representation: By removing suboptimal strategies, we narrow down the strategy set to only those that are relevant, reducing computational overhead and improving algorithmic efficiency.
Practical Examples in Adversarial Search: In the game of Tic-Tac-Toe, SEDS can be used to identify and remove suboptimal moves, like choosing a corner over the center when the latter opens up more winning paths. This simplifies the AI's search space, making it more efficient at finding the best move, especially in more complex variations of the game.

Evaluation Functions
Purpose of Evaluation Functions
Evaluation functions serve as the cornerstone for decision-making in adversarial search algorithms. These functions take a given game state and return a numerical value representing the utility or "goodness" of that state for a specific player. Essentially, they provide a heuristic estimate of the expected outcome, acting as a proxy for the actual utility function when it is computationally infeasible to calculate the exact value.
Examples: Chess, Go, Tic-Tac-Toe
In chess, the evaluation function gauges factors like material balance and king safety. For Go, it considers territorial control and group stability. In Tic-Tac-Toe, a simpler game, the evaluation function for the computer player ‘X’ can be as straightforward as:
where X2 and O2 are counts of almost-complete lines for 'X' and 'O', respectively. The function rewards configurations where 'X' is closer to winning by a higher margin. 3×X2 significantly boosts the evaluation when 'X' has two in a row without any 'O', and X1 adds a minor boost for potential future winning spots. Similarly, the function penalizes configurations that would allow 'O' to win in the next move or create a winning setup. 3×O2 significantly lowers the evaluation score when 'O' has two in a row without any 'X', and O1 subtracts a minor amount for potential future threats.
Building an Effective Evaluation Function
Creating an effective evaluation function requires a nuanced understanding of the game dynamics and a strategic approach to weighting different elements of the game state. The evaluation function should be:
Fast to Compute: Given that the function will be called frequently, it needs to be computationally efficient.
Accurate: The function should provide a close approximation of the true utility of the game state, as this directly impacts the quality of the search algorithm's decisions.
Adaptive: As strategies evolve or as new information becomes available, the function should be flexible enough to adapt to these changes.
Context-Aware: In some cases, the importance of specific factors may change depending on the game phase (e.g., opening, middle game, endgame) or other contextual cues.
By focusing on these attributes, developers can fine-tune evaluation functions to improve the performance and adaptability of adversarial search algorithms.
Dealing with Uncertainty
In the world of adversarial search, not all games come with complete and perfect information. When elements of randomness or incomplete knowledge are introduced, we enter the domain of games with uncertainty. The presence of uncertainty adds layers of complexity to decision-making algorithms, requiring adjustments to traditional techniques. In this section, we'll examine some approaches for dealing with uncertainty in adversarial search scenarios.
Stochastic Games
Stochastic games incorporate elements of randomness, making it challenging to predict the exact outcome of a move. For example, in poker, the shuffle of the cards is a stochastic event that affects all players. One approach to handling this randomness is by averaging out the expected payoff over all possible outcomes, often called the expected value.
Expectiminimax Algorithm
A direct extension of the Minimax algorithm, Expectiminimax, is designed to work under conditions of uncertainty. This algorithm assumes that chance nodes, representing random events, are introduced into the game tree. At each chance node, an expected utility is calculated based on the probabilities of different outcomes, which is then used to make decisions at decision nodes.
Bayesian Approaches
When the game incorporates elements of incomplete information, Bayesian methods can be applied. By using a probability distribution to represent the uncertain elements, these methods update the distribution as new information is gathered. This approach can model the uncertainty about an opponent's strategy or hidden game states effectively.
The introduction of uncertainty into adversarial search scenarios necessitates adaptations and innovations in algorithmic techniques. Whether we're contending with the randomness of card shuffles in poker or the uncertainty of an opponent's strategy in geopolitical simulations, approaches like Stochastic Games, Expectiminimax, and Bayesian methods offer robust solutions for tackling these complex challenges.
Real-World Applications
Adversarial search doesn't exist in a vacuum; it has meaningful applications in various domains, proving its utility far beyond the realm of board games and theoretical constructs. Here we'll explore some critical areas where adversarial search plays a crucial role.
Finance: High-Frequency Trading
In the competitive landscape of financial markets, the ability to predict and adapt to other traders' strategies can offer a significant edge. Adversarial search algorithms can simulate various market conditions and opponent behavior, allowing high-frequency trading systems to optimize their buy/sell decisions in real-time.
Cybersecurity: Defensive and Offensive Strategies
The cybersecurity landscape is essentially a battleground where attackers and defenders continually adapt their tactics. Adversarial search algorithms can model potential attacks and vulnerabilities, enabling proactive defense mechanisms. Conversely, these algorithms can also be used to stress-test security systems by simulating advanced cyber-attacks.
Healthcare: Medical Treatment Strategies
In medical decision-making, the "opponent" can often be the disease itself, which also "adapts" by developing resistance to treatments. Adversarial search can model different treatment strategies and predict how diseases might evolve in response, thereby guiding more effective treatment protocols.
Autonomous Vehicles: Navigating Complex Environments
The world is a complex, ever-changing puzzle for autonomous vehicles. They must anticipate actions from other drivers, pedestrians, and even wildlife. Adversarial search can provide a framework for these vehicles to evaluate millions of potential scenarios in split seconds, making better decisions and improving road safety.
Sports Analytics: Game Strategy
Whether it’s basketball, soccer, or almost any competitive sport, adversarial search algorithms can simulate countless scenarios and strategies, providing coaches and players valuable insights into optimal plays and tactics. These algorithms can evaluate the ‘game tree’ in real-time, offering strategic advice that can be the difference between a win and a loss.
E-commerce: Dynamic Pricing
In the competitive world of online retail, dynamic pricing strategies can make or break a business. Using adversarial search algorithms, e-commerce platforms can anticipate competitor pricing changes and customer reactions, allowing them to optimize their pricing strategies for maximum profit and market share.
Advanced Topics
As we delve deeper into the realm of adversarial search, it becomes evident that the basic algorithms and evaluation functions only scratch the surface. With the rapid advancements in AI and machine learning, new paradigms are continually emerging, pushing the boundaries of what we can achieve in adversarial settings. This section explores some of the cutting-edge techniques that promise to revolutionize the field.
Multi-Agent Reinforcement Learning
What is It: A framework where multiple agents learn by interacting with an environment and each other.
Why It Matters: Enables more realistic modeling of adversarial scenarios that involve more than two players or are not strictly zero-sum.
Applications: Utilized in simulations, robotics, and even complex board games.
Neural Networks and Adversarial Search
What is It: The use of neural networks to approximate complex evaluation functions or even the search process itself.
Why It Matters: Allows for the handling of problems too complex to be solved through traditional algorithms or evaluation functions.
Applications: Pioneered by systems like AlphaGo, neural networks have shown exceptional prowess in games like Go, Chess, and Poker.
The Role of Heuristics
What is It: Techniques that provide practical shortcuts in decision-making.
Why It Matters: Can drastically reduce computational cost, enabling real-time decision-making in complex games.
Limitations: While heuristics can be incredibly useful, they are not guaranteed to find the optimal solution and can sometimes lead to errors.
Advanced Tree-Search Techniques
What is It: Enhancements to traditional tree-search methods, like Progressive Widening, UCT (Upper Confidence Bound for Trees), and Tree-Strap.
Why It Matters: These techniques make large-scale and computationally intensive problems more tractable.
Applications: From video games to strategic simulations in military and economic planning.
Game Abstraction Techniques
What is It: Simplifying the game model to make it computationally easier to solve.
Why It Matters: Allows for quicker solutions at the expense of some accuracy.
Methods: Includes techniques like state aggregation, action abstraction, and the aforementioned "successive elimination of dominated strategies."
Quantum Computing and Adversarial Search
What is It: The use of quantum algorithms for solving games.
Why It Matters: Has the potential to solve games of unprecedented complexity.
State of the Field: Still largely theoretical, but research is ongoing.
Conclusion
Adversarial search stands as a captivating intersection between game theory and artificial intelligence, providing a rigorous framework for handling competitive scenarios where multiple agents vie for conflicting goals. Through our exploration of its foundational algorithms, evaluation methods, and real-world applications, we've glimpsed the profound implications this concept has for decision-making systems.
From traditional games like chess to intricate applications in finance and cybersecurity, adversarial search algorithms are proving their mettle by delivering increasingly sophisticated and effective solutions. The landscape becomes especially compelling as we introduce more advanced topics like multi-agent reinforcement learning and neural network-based strategies. These techniques not only push the boundaries of computational efficiency but also challenge us to consider complex ethical implications.
As we've seen, adversarial search isn't just about winning games; it's about optimizing decision-making in complex, dynamically changing environments. Whether it's a trading algorithm analyzing market fluctuations or a healthcare model deciding the best treatment strategy, the principles of adversarial search can offer invaluable insights.
Challenges persist, particularly around computational complexity and ethical considerations. Yet, as AI technology continues to evolve, so too will our strategies for navigating adversarial landscapes. Future research promises exciting developments, further integrating game theory and AI to solve increasingly complex problems.
Thank you for joining us on this intellectual journey. Adversarial search is but one of many fascinating realms within AI, and we encourage you to continue exploring. Whether you're a seasoned expert or a curious novice, the fields of game theory and artificial intelligence offer a wealth of knowledge waiting to be discovered.
Stay tuned for next week's post, where we'll delve into the code behind Successive Elimination of Dominated Strategies (SEDS) and adversarial search algorithms like minimax to enhance your game AI.
References:
Russell, S. J. and Norvig, P., Artificial Intelligence: A Modern Approach, 4th Edition, Prentice Hall, 2021
Dynamic pricing of differentiated products with incomplete information ... (n.d.). https://ietresearch.onlinelibrary.wiley.com/doi/epdf/10.1049/cim2.12050
Investors may take heart: A game theoretic view of high frequency trading. (n.d.-b). https://www.researchgate.net/profile/Vivek-Pandey-10/publication/280883403_Investors_may_take_heart_A_game_theoretic_view_of_high_frequency_trading/links/55ca670d08aea2d9bdcc0061/Investors-may-take-heart-A-game-theoretic-view-of-high-frequency-trading.pdf



